I was looking for info on the properties of pentagons for a geometry question in my textbook.
In textbook, we are given a pentagram (5 sided star) drawn inside a regular pentagon (equal sides) and have to work out the angles.
Image source: maths.surrey.ac.uk |
Therefore all of the angles along the pentagon are 36 degrees.
I double checked this with my protractor (which was not part of the question) and they are 36 degrees. I also checked the other angles and they are either 72 degrees of 108 degrees.
This diagram has information on it that confirms this deduction i.e Other angles within the pentagram would be multiples of 36 i.e. either 72 degrees or 108 degrees depending:
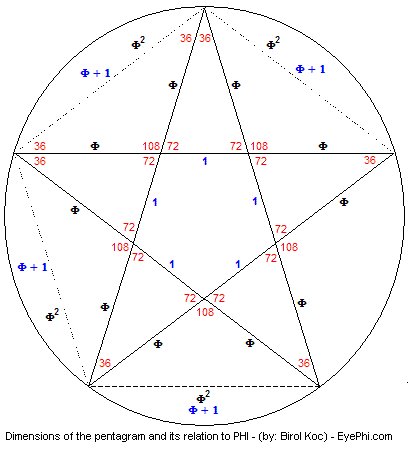
This is another image I found:

What was interesting is this image I found where the concept is repeated again in the centre and again.
Image source: aleph0.clarku.edu
This is all based on all the sides being equal and so all the angles being equal.
I found the info below on http://www.mathopenref.com/pentagon.html
Properties of regular pentagons
| Interior angle | 108° | Like any regular polygon, to find the interior angle we use the formula (180n–360)/n . For a pentagon, n=5. See Interior Angles of a Polygon |
| Exterior Angle | 72° | To find the exterior angle of a regular pentagon, we use the fact that the exterior angle forms a linear pair with the interior angle, so in general it is given by the formula 180-interior angle. SeeExterior Angles of a Polygon |
| Area | 1.72 S2 approx | Where S is the length of a side. To find the exact area of a regular pentagon or any regular polygon, using various methods, see Area of a Regular Polygon and Area of an Irregular Polygon |
Properties of all pentagons
| Number of diagonals | 5 | The number of distinct diagonals possible from all vertices. (In general ½n(n–3) ). In the figure above, click on "show diagonals" to see them. See Diagonals of a Polygon |
| Number of triangles | 3 | The number of triangles created by drawing the diagonals from a given vertex. (In general n–2). In the figure above, click on "show triangles" to see them. See Triangles of a Polygon |
| Sum of interior angles | 540° | In general 180(n–2) degrees . See Interior Angles of a Polygon |
There is also some info on pentagons/pentgrams and crop circles here: http://www.axve02.dsl.pipex.com/cropcirc/chap5/Pentagram.htm
Even more about pentagrams: http://mathworld.wolfram.com/Pentagram.html
http://www.anselm.edu/homepage/dbanach/31-drawing.htm (This includes various drawings as well as pentagrams)
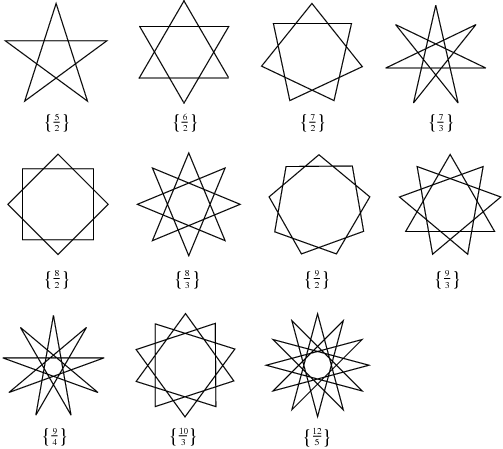 Image Source: http://mathworld.wolfram.com/Pentagram.html
Image Source: http://mathworld.wolfram.com/Pentagram.html
Other info on the pentagons, pentagram and organisations:
USA Pentagon Building
Free masons - Pentagram (5 senses)
See this page: http://www.lakeharrietlodge.org/lhl277/MainMenu/Home/MasonicEducation/TheSymbolismofthePentagram/tabid/413/Default.aspx
Sacred Geometry: http://www.esotericonline.net/group/sacredgeometry/forum/topics/sacred-geometrythe-pentagram?commentId=3204576%3AComment%3A9364&groupId=3204576%3AGroup%3A9042
http://www.anselm.edu/homepage/dbanach/31-drawing.htm (This includes various drawings as well as pentagrams)
Other info on pentagrams:
The pentagram, is also called the 5-point star, pentacle, pentalpha, or pentangle, is the star polygon  .(See diagram below).
.(See diagram below).
It is a pagan religious symbol that is one of the oldest symbols on Earth and is known to have been used as early as 4000 years B.C.
The first known uses of the pentagram (the simplest regular star polygon) are found in Mesopotamian writings dating to about 3000 BC. The 5 points represented the 5 astrological directions associated with Jupiter, Mercury, Mars and Saturn, and Venus.
It is a symbol with its roots in alchemy and in the ancient mysteries. The metaphorical interpretation of geometric figures goes back to Pythagoras and the beginnings of philosophy.
In alchemical symbolism the five points signify the interconnection of the four elements (Air, Fire, Water, and Earth) united by the fifth element or "quintessence" that is sometimes called Aether and more often Spirit.
In alchemical symbolism the five points signify the interconnection of the four elements (Air, Fire, Water, and Earth) united by the fifth element or "quintessence" that is sometimes called Aether and more often Spirit.
The pentagram is used in traditional Chinese medicine and Taoism too, which employs a system of five elements rather than four (Water, Wood, Metal, Fire, Earth). The fact that we have five digits on each of our hands and feet is another way that five becomes a mysterious number signifying humanity. More recently, the pentagram has been widely publicized as the chief symbol of Wicca
Other star polygons:

Other info on the pentagons, pentagram and organisations:
USA Pentagon Building
Free masons - Pentagram (5 senses)
See this page: http://www.lakeharrietlodge.org/lhl277/MainMenu/Home/MasonicEducation/TheSymbolismofthePentagram/tabid/413/Default.aspx
Sacred Geometry: http://www.esotericonline.net/group/sacredgeometry/forum/topics/sacred-geometrythe-pentagram?commentId=3204576%3AComment%3A9364&groupId=3204576%3AGroup%3A9042
I find your research very interesting on many of your posts.
ReplyDeleteIn particular, this is a unusual question that I have not seen before i.e. a pentagram inside a pentagon. Which maths book are you working from? I saw form a previous post of yours that you were using a KS3 textbook?
I found your research very interesting!How your investigation tied up your maths question with a general background and links to the pentagram and pentagon shows an education, in more than maths itself!
It is good to have a general knowledge and the world both past and present have been made up of many things. To have a basic knowledge of these, is useful is nothing else - the world and its existence is far more than what one learns at school. Just to know of their existance and not take that any further is to know more than the vast majority of other school pupils.
I also noticed your link to sacred geometry. Who would have thought that maths and geometry could be sacred? I often wondered of the practical use of many aspects of maths? I found your post most interesting and it does indicate a deepness to maths. Even if it is historical or esoteric.
Who would have known these things from a school maths education point of view.
I always notice that homeschoolers have a far wider general knowledge and learn about far more things.